After finishing my previous project, I still found myself with plenty of time in-between classes (thankfully I’m only taking 4 courses this semester as opposed to my usual 6, so hopefully this trend continues throughout the semester). Also, as I recently took up a UTA position for CS2505 at VT (Intro to Comp Org), I found myself with plenty of down time on-shift as the early assignments are easy and most students don’t need help as of yet. Thankfully, some friends come and spend time with me to make the time go by faster. One of these friends typically brings a Go board along with her and loves to play connect 5 with us (think tic-tac-toe, but on a Go board, and you have to connect 5 instead of 3). After countless games, I thought back to my minimax algorithm for tic-tac-toe (here), and wondered if it applied smoothly to connect 5. And so, I decided to start working on this project.
First was to create the game. I was drawn to Java because I’m most comfortable working with object-heavy projects in Java (as opposed to something like Python). Coding the basic game was simple. The board itself is basically an 18×18 tic-tac-toe board. As such, I just used a 2D integer array size 18×18 and used constants for black, white, and empty spaces. I used swing for rendering, and KeyListeners for user input. Arrow keys navigate and enter places a piece. Upon placing a piece, control is handed over to the AI to decide the move they are going to take.

Empty gameboard. The cursor is indicated with the red square (moves with arrow key input). As you’ll see later, the blue cursor (not shown here) indicates the previous move.
Next came calculating the heuristics for scoring any given board. I used this post by Ofek Gila as a foundation and built on that. Essentially, the board is traversed in every direction (horizontal, vertical, topleft->bottomright diagonal, topright->bottomleft diagonal) and consecutive pieces are counted and scored, with the sum total being the overall score of the current board state. The scores for consecutive pieces are based on the perceived value of that shape (i.e. a 5 in a row is worth much more than a single piece). I wanted this version to play very defensively (an annoying strategy for veterans of the game), so there are noticeable score differences based on what the color of the consecutive pieces is. Afterward, I began writing the minimax algorithm. The basic jist of minimax is to look a set number of moves into the future, score the current board state, and play off of the assumption that your opponent is going to make the best move for them at their given board state (hence the name minimax — you’re trying to maximize your gains and the opponent is trying to minimize them). I settled on looking 2 moves into the future, as it fit the balance of running quickly and decent decision making. If you want to learn more about minimax, feel free to look at the code for this project (link at the bottom).
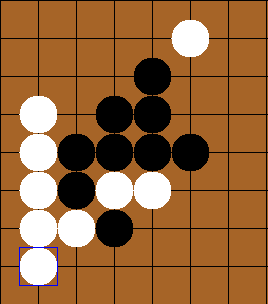
Using minimax, the AI (white) was able to defeat the user (black) here, while also stopping a win for black (if the white piece at the upper-right was not placed, black would have won)
Using this method, I ran into a couple of speed bumps. The major issue was performance. Especially at the beginning of the game, even after the user’s move, there are still 323 possible moves (18^2=324, -1 for the placed piece). That in addition to looking n moves into the future, meant that there are about 323^n checks that the algorithm needs to make (the number is actually slightly less than 323^n, as it doesn’t factor in placing new pieces and repeating the process, but it is essentially that value for small values of n, so we will ignore it for this basic analysis). To solve this, I cropped the board down to only ‘relevant’ spaces (I defined relevant here as any space around all of the current pieces in play with a buffer of 2 spaces on every side). Using this method, I was able to reduce the number of checks for 2 moves from 323^2=104,329 to 25^2=625 (placing one piece and creating a buffer of size 2 on every side creates a 5×5 grid, resulting in the 25 seen there (5^2 = 25)). Other than that, there is a bug in which the AI would let the player win if it won later down the decision-tree (in other words, it detected a win but didn’t take into account the opponent winning sooner). I expect this to be an error with scoring, but as I want to continue working on other projects, I will leave this bug in for now.
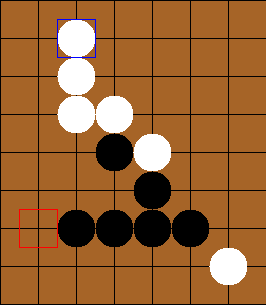
You can see that the AI (white) detected a win, so it ignored black’s 3 in a row, ensuring a win for black.
Testing this out on some of my friends, I found that it played fairly decently. However, due to some minor bugs in the score evaluation (detailed at the end of the previous paragraph), veterans could consistently beat the bot (albeit after hard, long-fought games). This project was a fun one that I could share with friends, so I definitely enjoyed working on it and seeing it get better along the way. I encourage you to download the project and try playing against it yourself. You can find the github for this project here.
Recent Comments