Admittedly, the time before my summer semester in Japan was ill-spent in regards to furthering my understanding in the Computer Science world. However, there were still a couple of projects that I did for fun before I left. This first project, a rather simple caesar cipher, was the first of two projects I did. I did this project in particular as a way to brush up on some of the knowledge of the C language I gained during my spring semester CS 2505 class at Virginia Tech. For those unfamiliar with the concept of a caesar cipher, it’s a crude way to encode a chunk of information — simply taking every letter and shifting it up or down a predetermined number of spaces in the alphabet. For instance, the string “abcd” would be encrypted to “bcde” with a caesar key of positive one. Of course, traditionally, wrapping occurs at the ends of the alphabet; meaning z -> a with a key of +1, and a -> z with a key of -1.
There are a couple key parts when it comes to translating this into code. First and foremost, I made it runnable via. the command line. The program expects the file path to the text file the user wants scrambled or unscrambled, along with either ‘e’ or ‘d’ for ‘encode’ and ‘decode’ respectively. Next, instead of letting the letters wrap once at the end/beginning of the alphabet, I allowed the characters to go above/below this limit, possible thanks to the format of the ASCII table.
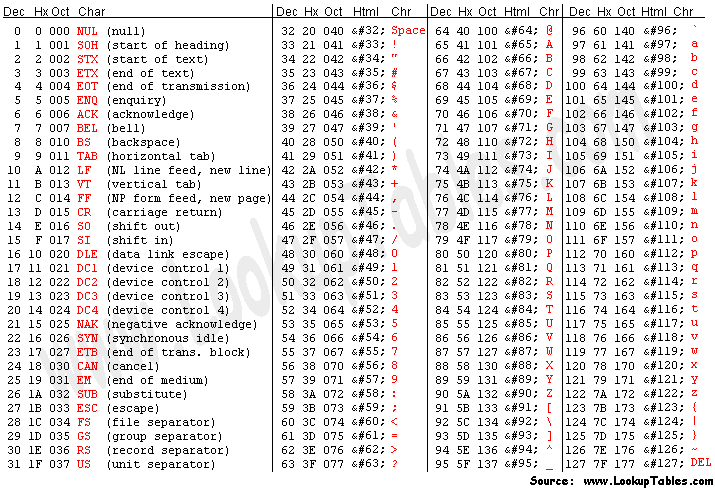
ASCII table
In C, along with the vast majority of programming languages used today, ‘char’ (character) variables are actually stored as integers. Each character is 1 byte, allowing for up to 256 different characters to exist. This not only includes your standard upper/lower case alphabet and numbers, but also special characters, along with some special, machine only characters, like ‘\n’ (new line). So, instead of wrapping at the ends of the alphabet, I wrapped at the ends of the ASCII table (see methods encode and decode in the block below to see how). In regards to my program, this is relevant because it allows for characters to spill over into generally weird or unexpected characters, making it easier on us to program because we don’t need to look for specific ASCII values to wrap around, as well as adding a bit more effectiveness to the final product. Of course, this method won’t fool someone who knows what they’re doing when it comes to decryption, but it should generally prevent friends or co-workers from snooping into information you don’t want shared.
There are still plenty of improvements that can be made to this system to improve it even further and lessen the chance of someone cracking a particular files key. As you can see in this iteration of the program below, the key is static between all files, meaning a correct guess on one file means access to your entire library of secret text files. This could be improved by simply making the key random between files and stored somewhere inconspicuous. For instance, the key could be between 0 and 255, and simply written as the first character of the encoded file. While again, this method would fail almost instantly in the case of a professional crack, it should stump the average Joe for a couple of hours. Or, perhaps this method is repeated for every character in any one file; the key for any given character placed just before or after it. I’m sure you can see how this method can become increasingly complex, and increasingly difficult to break, the longer you think about it.
FILE *f;
int caesar = 5;
int main(int argc, char **argv) {
if (argc != 3)
badInput();
FILE* f = getFile(argv[1]);
if (strcmp(argv[2], "e") == 0)
encode(f);
else if (strcmp(argv[2], "d") == 0)
decode(f);
else
badInput();
fclose(f);
return 0;
}
void badInput() {
printf("Format is '.../caeser <.../fileToEdit.txt> <e/d>'\n");
exit(1);
}
FILE* getFile(char *url) {
FILE *f = fopen(url, "r+");
if (f == NULL) {
printf("Can't locate file '%s'", url);
badInput();
}
return f;
}
void encode(FILE *f) {
int c;
while((c = fgetc(f)) != EOF) {
fseek(f, -1, SEEK_CUR);
fputc((c + caesar) % 255, f);
fseek(f, 0, SEEK_CUR);
}
}
void decode(FILE *f) {
int c;
while((c = fgetc(f)) != EOF) {
fseek(f, -1, SEEK_CUR);
fputc((c - caesar) % 255, f);
fseek(f, 0, SEEK_CUR);
}
}
The C code behind the Caesar Cipher. If you have any questions about the code feel free to email me: [email protected].
This project was an easy, quick, and fun way to stay familiar with the ins and outs of ASCII values and C I/O alike. Feel free to take this idea further and create ciphers of your own!

Recent Comments