I recently read a book titled The Golden Ticket by Lance Fortnow in which the P / NP Problem and its importance to the theory of Computer Science are heavily discussed. Explained briefly, the P / NP Problem asks if every single problem can be solved quickly and efficiently. In relations to cryptography, P / NP is crucial because it allows for the creation of hard math problems to, for example, be able to hide private information on a public network. One of the most famous P / NP Problems, the Clique problem, was discussed and is, in my opinion, one of the more intriguing problems in the book.
Take, for example, a society called Frenemy, in which every citizen either has a 50% chance to be friends or a a 50% chance to be an enemy with a person they just met. In Fortnow’s book, he details how it would be virtually impossible to find all cliques of varying sizes (difficulty/time to find all cliques increases as size of desired clique increase) inside of this society (A clique is a group of people in which everyone is friends with all other members). At first, I didn’t think it would be that difficult to find the largest clique, but after making a simulation for myself, I was proven otherwise.
I stayed true to the Frenemy rules in my simulation – every time someone meets someone else, they have a 50% chance to either be their friend or their enemy. I experimented with varying population sizes as well as varying amounts of citizens in which each person can meet. I made two methods in order to experiment, one in which everyone meets everyone else in the society, and one in which everyone meets everyone on their own street (9 total streets in which 1/9 of the total population lives on each given street). To make the data easier to set up and understand, each citizen is given an identification number as well as an ‘address’, the number of street they live on. I aimed to find every single clique of size 3 in the society, and to see for myself how difficult it became to find them as population size increased.
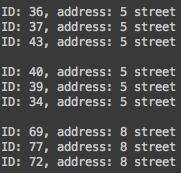
A couple of cliques present in a population size of 100 in which citizens met everyone on their own street.
I found that the total time to generate the population and find cliques of size 3 took much much longer the higher the population size was, which makes sense in hindsight. Adding a single citizen to a population size of 20 where everyone meets everybody doesn’t have nearly the impact as adding a citizen to a population size of 10,000, as the number of updates a computer has to make to each citizen’s list of friends and enemies for a population of 10,000 is much larger. When I was reading Fortnow’s book, I didn’t put much thought into the rate at which the updates change as population size grows. I naively thought growth was generally linear, allowing total computations to find all cliques of size 3 to be relatively small compared to the actual value. Only after I made my own simulation did I truly understand the difficulty surrounding finding a solution to the Clique problem. If you find find yourself with some free time, I would recommend making a simple simulation like this for yourself so you can see the results firsthand.
I’d like to thank Lance Fortnow for pushing me to explore this problem through his book, as all P / NP problems (not just the Clique problem) are profoundly interesting in their own rights. And, if you’re planning to look more into the P / NP problem, Lance Fortnow’s The Golden Ticket is a must read. The discussion as well as the existence of the P / NP Problem has really expanded my understanding of Computer Science and the importance of not only the physical act of coding, but the theory behind CS as well.


Recent Comments