The 2015 school year was when I began dabbling around AI. The idea always amazed me. Everything from movie depictions of them to the real practical uses they have in modern day life was interesting, and I wanted to know more about it.

During the holiday break, I decided to dedicate my programming efforts towards learning Neural Networks. I knew a little bit about them before hand, like the architecture and the theory of how they worked, but had no idea how to implement them into my own projects. The wall avoider project was dedicated towards making a very, very simple Neural Network that progressively got better at avoiding walls using a genetic algorithm.

But first, I will briefly explain what Neural Networks are. In short, they are systems modeled after the human brain – that is, they use a set of ‘neurons and synapses’ that manipulate a given set of input data so that a desired output is reached. The issue is, however, that we do not know the correct weights and values necessary so that the network will give us our desired output. There are several ways of determining error/finding the best set of values so that a desired output is reached. For this project, I’ll be using a genetic algorithm to essentially determine the best network, and ‘breed’ it with other good networks, resulting in an equally if not better Neural Network. This occurs by choosing 2 Neural Networks that result in a long run (doesn’t hit the wall) and randomly choosing weights from both networks to result in a new Neural Network.

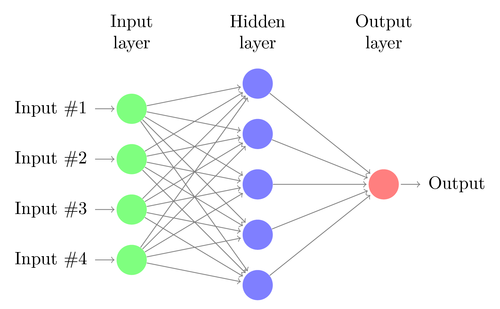
Anatomy of a Neural Network.

My project’s Neural Network has 3 input nodes and 1 output node. The value of the input nodes is either a 1 or a 0, depending on whether or not its respective ‘eye’ (line extending from the center of the runner) hits a wall or not. These values are each multiplied by their respective weights (random at first, then altered through the genetic algorithm) and summed together, then put through an activation function. In my example I used a variation of a sigmoid function (1 / (1 + e^(-x)) as an activation function. Sigmoid functions are nice because their ranges are typically (0,1), resulting in either an ‘on’ or an ‘off’ setting. If the a(x) > 0.5, it turned right. If a(x) < 0.5, it turned left. If a(x) = 0.5, it didn’t turn at all.

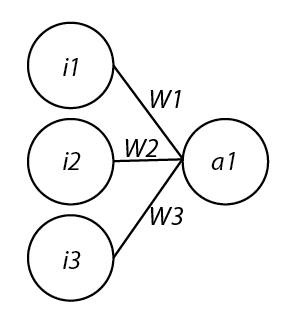
Graphic of my Neural Network. i = input (eyes), W = weights, a = activation

After constructing this system, I began running tests. As the objective wasn’t a hard one to learn, the networks involved mastered the challenge quickly. In the gifs, you can see on the left the trial number and the fitness value (how well the network is doing) for each member of the population. p# = parent, c = child, and ^ indicates current best network.

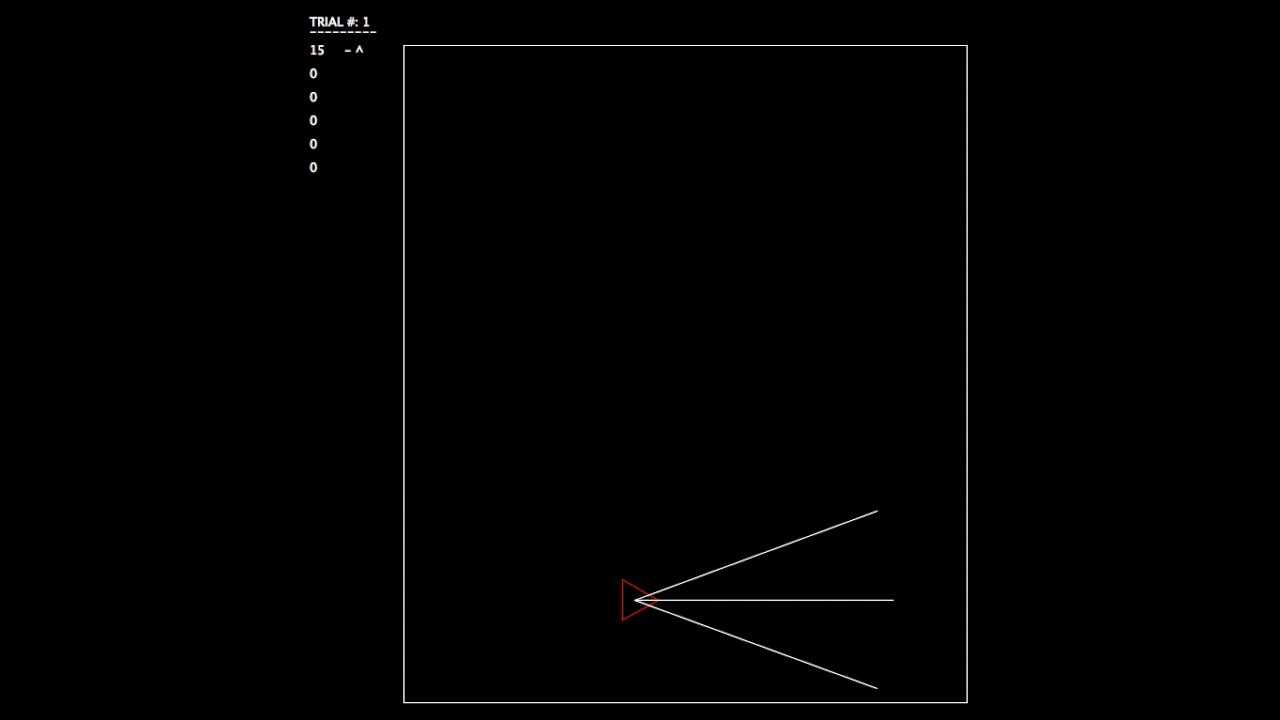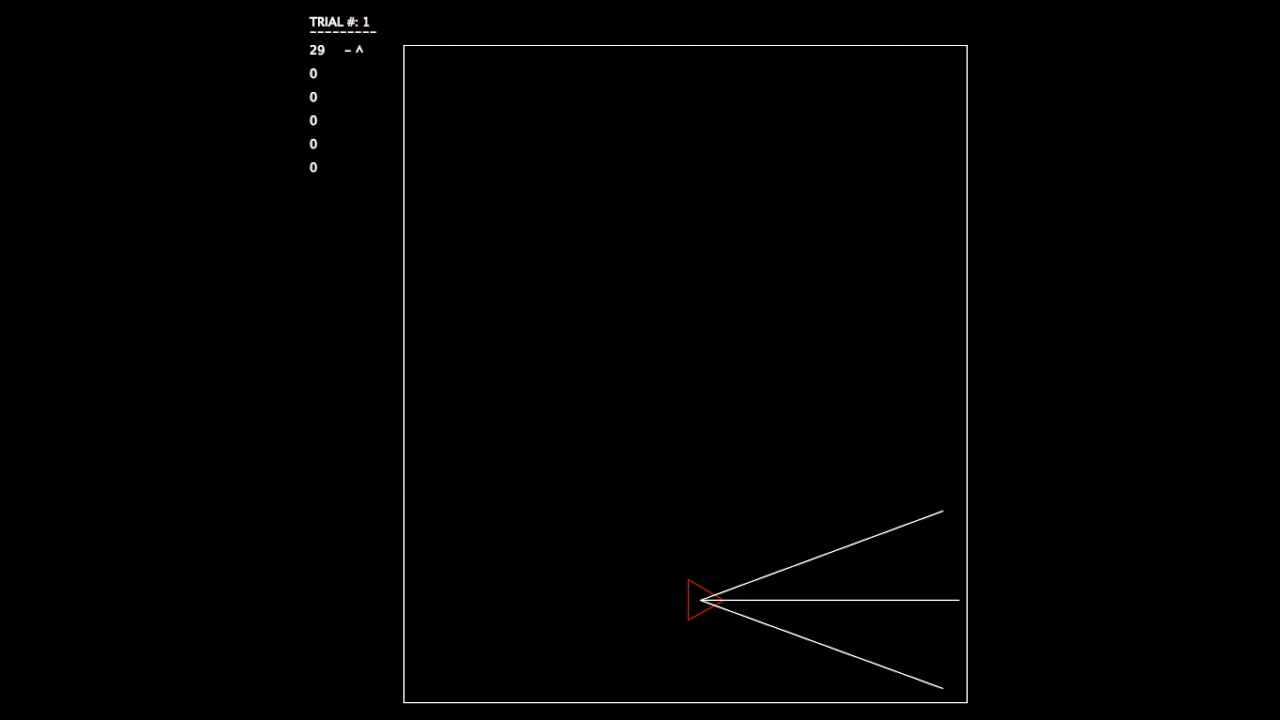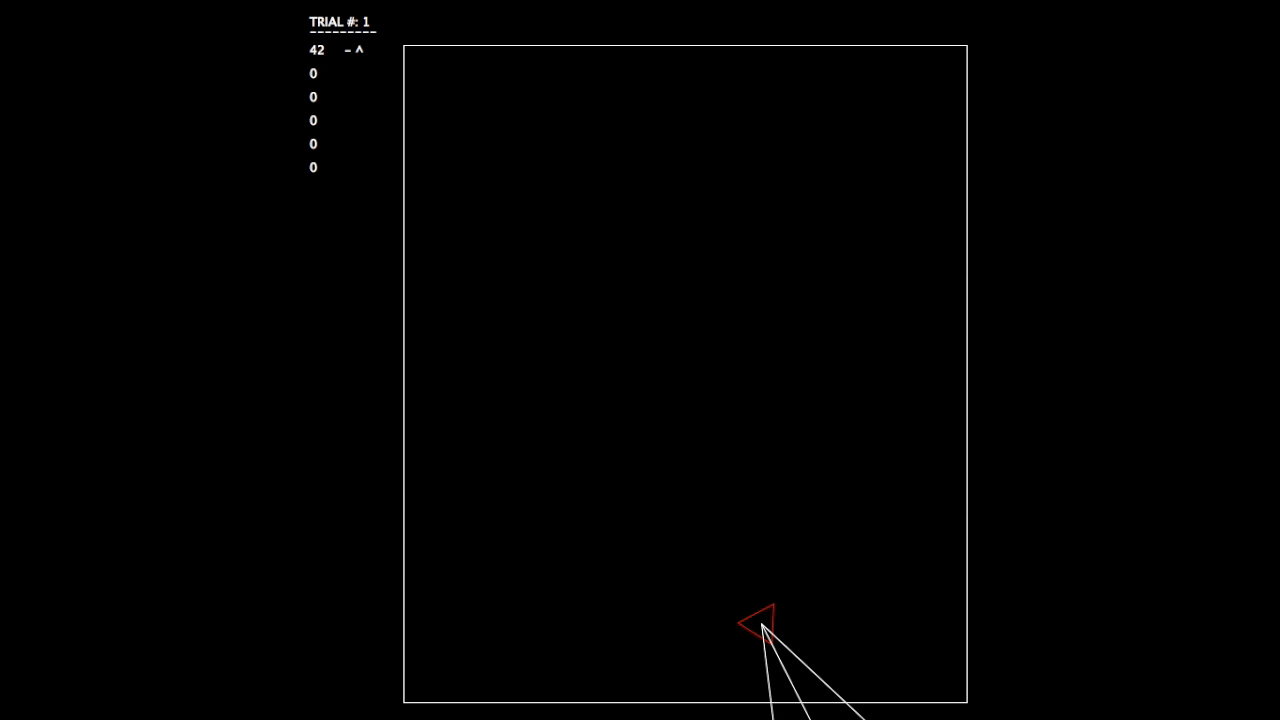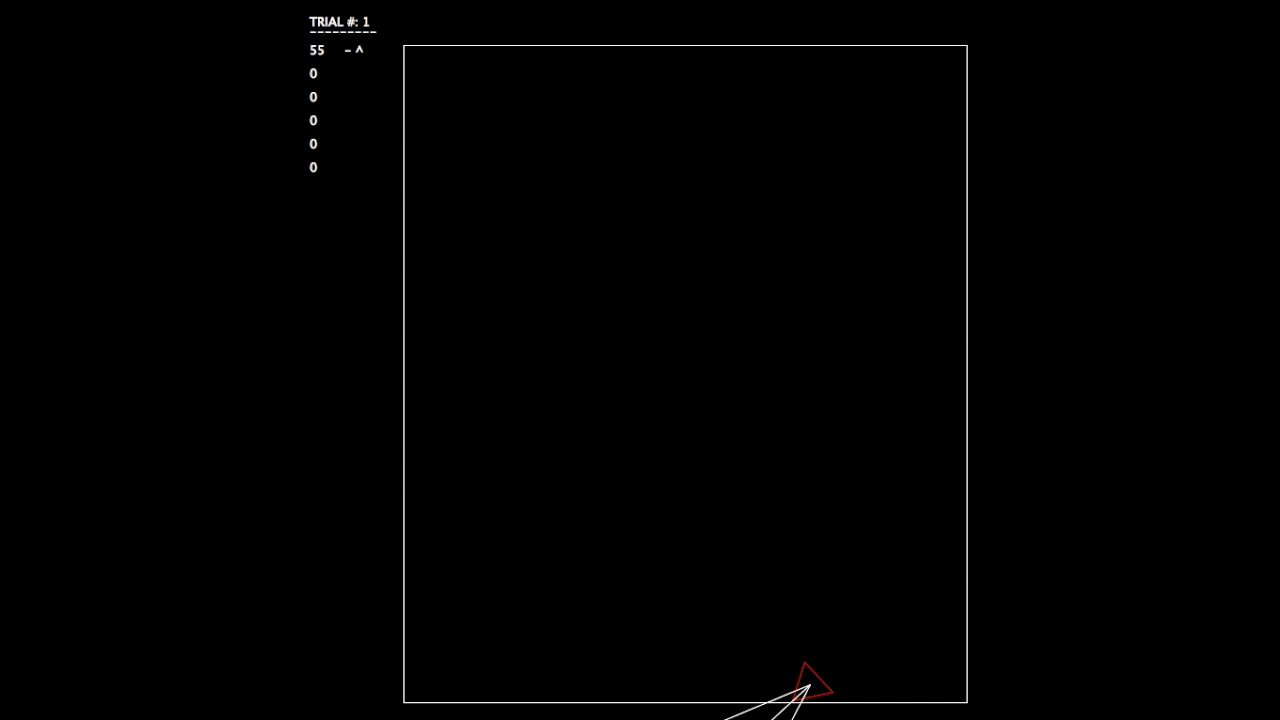
Trial 1, struggling.

Trial 7, a pretty decent network is bred, but still room for improvement.

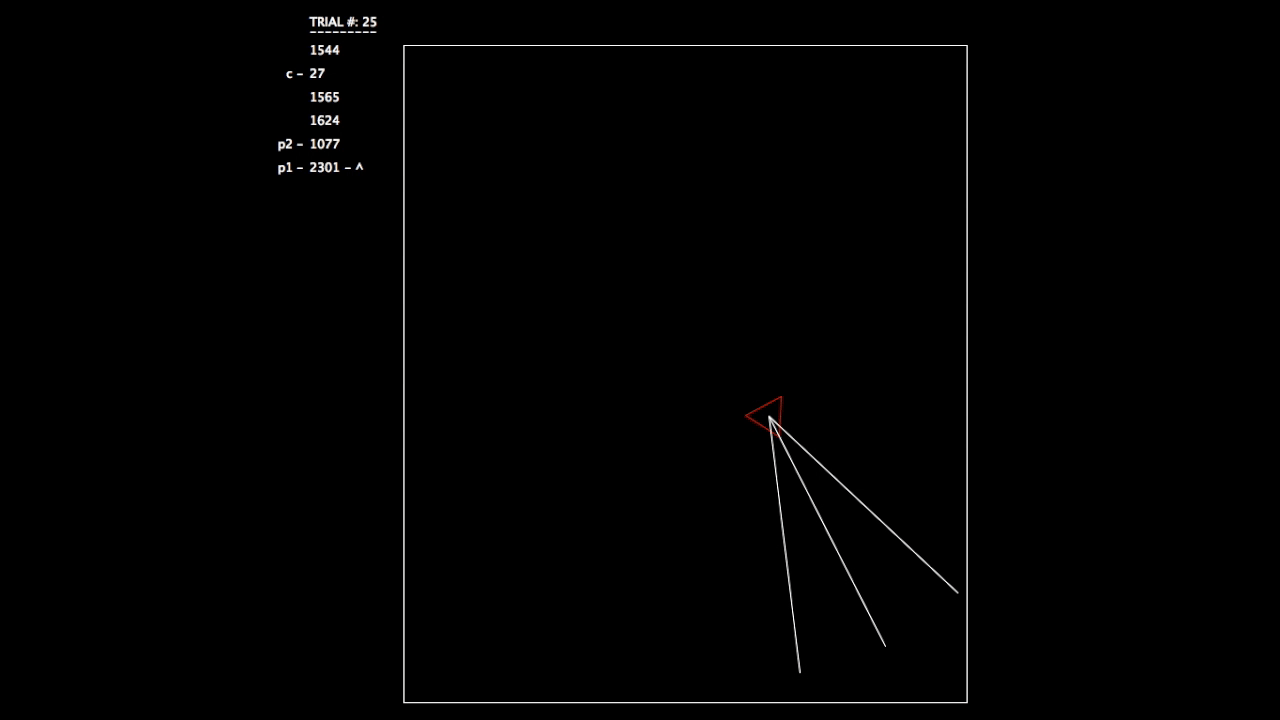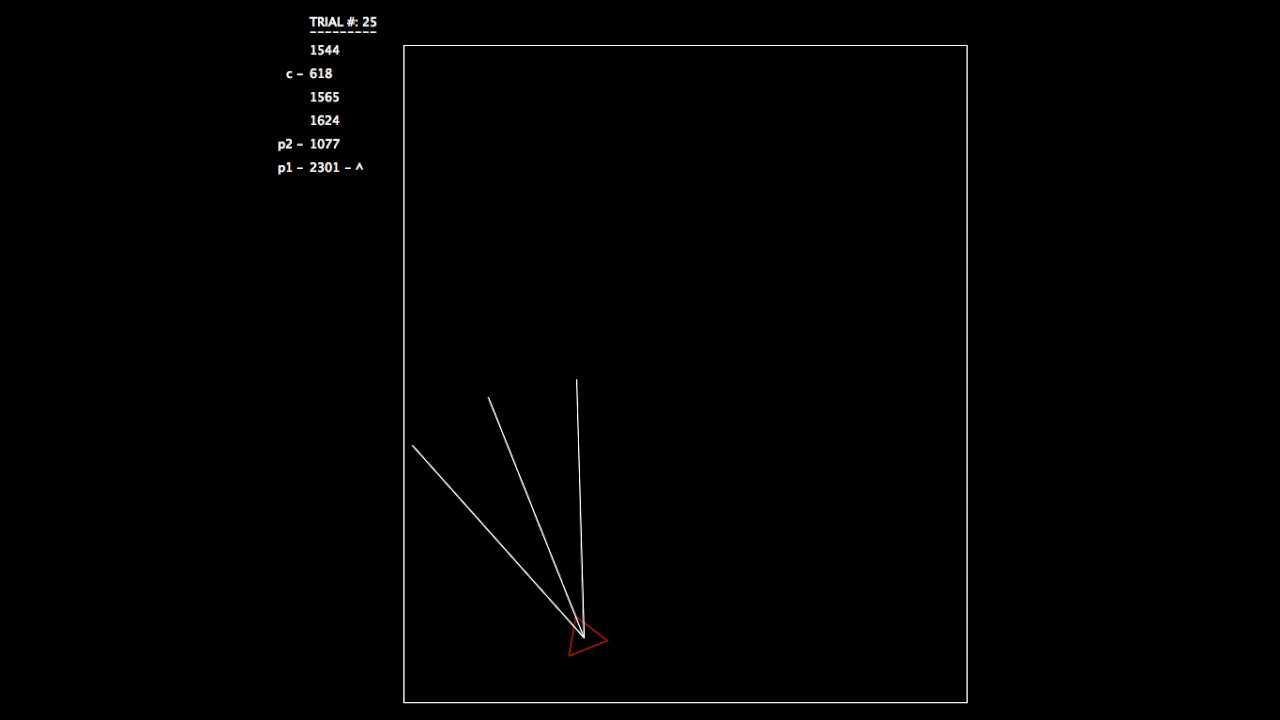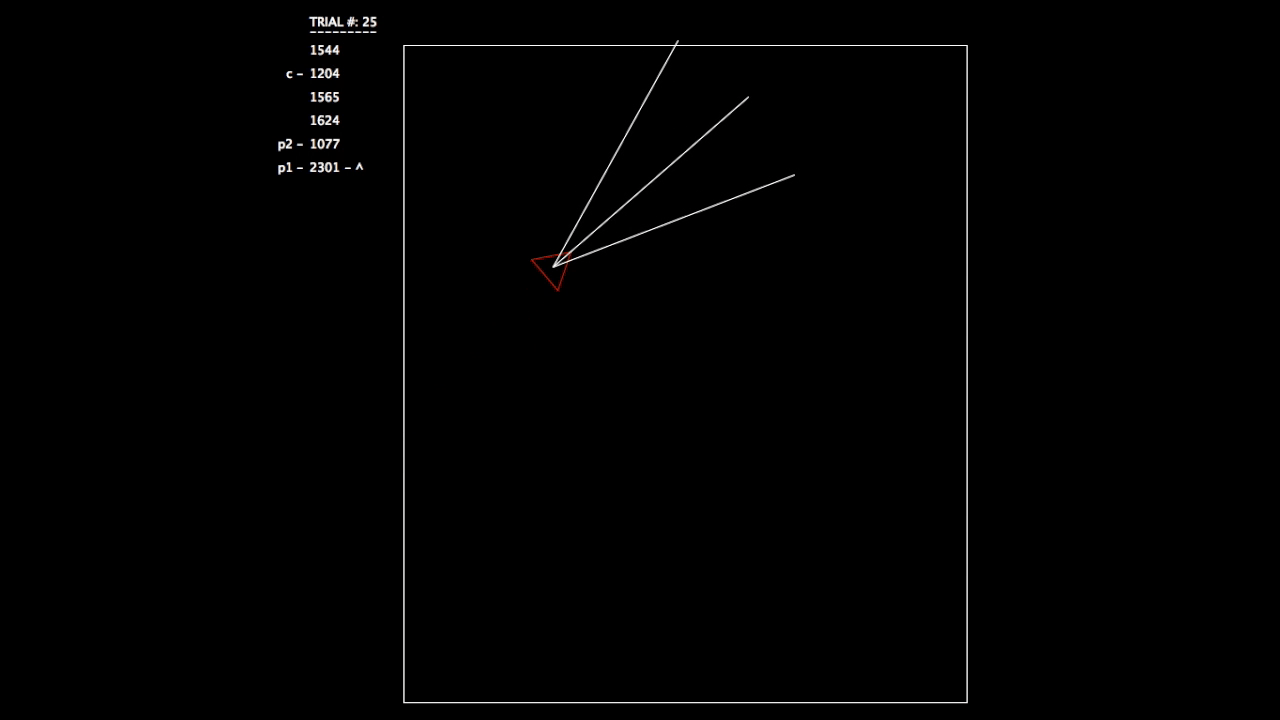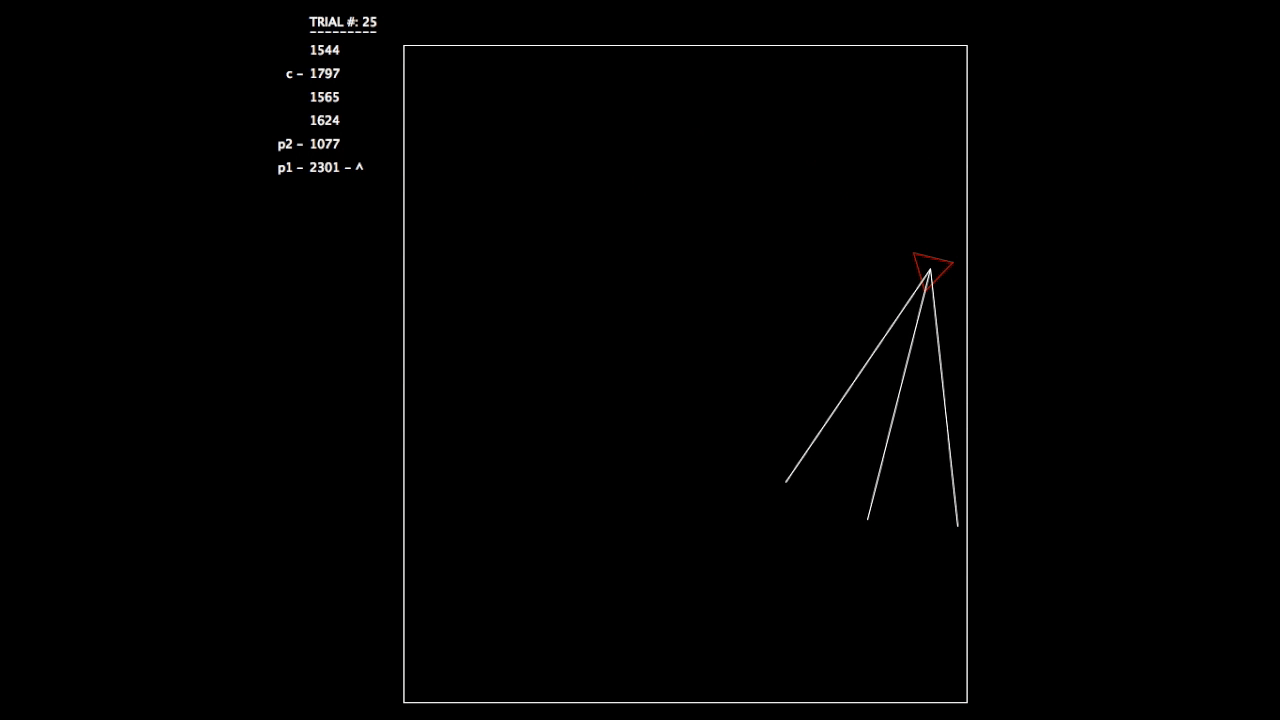
Trial 25, all networks are doing very well.

This was a great intro to Neural Networks. I definitely want to take this idea further and create deeper, more complex networks for harder tasks.

If you want the source code, you can get it here (Java, 26kb): https://drive.google.com/file/d/0Bz_0wgRmDpKqSVRvbXpzcm1VRVE/view?usp=sharing